
今回為大家介紹一種新出爐的數多酷 “遊戲局” 叫 「同盤局」。
圖一是一個卅一個亮字旋轉對稱的遊戲和它的答案。圖二是另一個遊戲和它的答案,它亦有卅一個亮字但是對稱的。
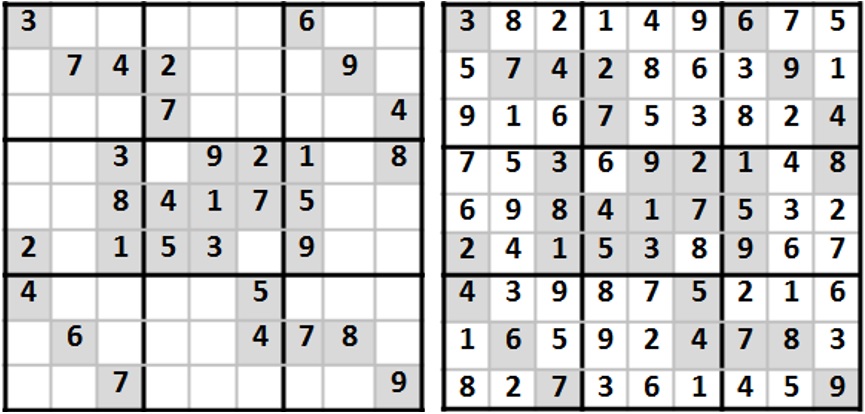
(圖一左:一局遊戲;圖一右:圖一局答案)
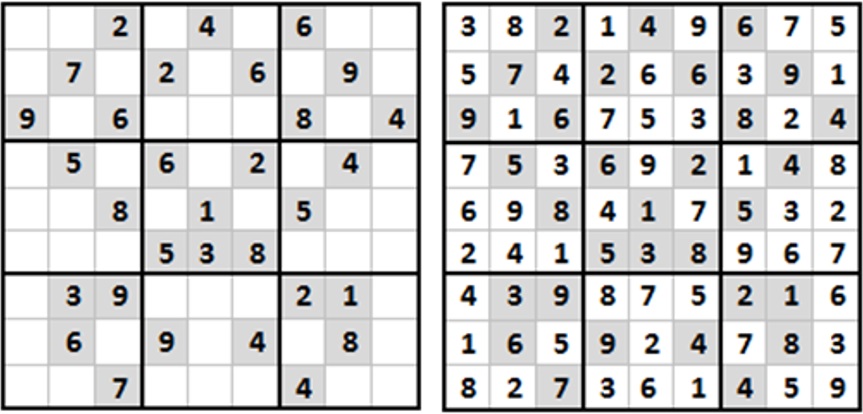
(圖二左:一局遊戲;圖二右:圖二局答案)
把兩局(圖一和圖二)遊戲的 “答案底盤” 擺在一起 (圖三),掃走亮字灰色格底 (圖三,中),你馬上發覺它們的答案底盤原來同出一轍。所不同的,只是所選亮格不同分佈 (卅一亮字只是偶合),但八十一個數字的原字位不變。因此,兩個答案底盤基本同出自一個 “組合盤”。
(圖三左右:原兩遊戲的答案底盤;圖三中:它們的組合盤)
有趣的問題來了,數多酷也好,數獨也好,九方 “八十一格” 有多少個 “組合盤” 呢?這是一個有數可計的問題,早有人它計算了出來,是個天文數字!雖然因為有對稱性的出現,使結果打了個折扣,它的數目還是非常龐大,我在前文也說過了,不再累贅,反正,仍是一個十六個零的天文數字! 上文耍弄,我已簡單地說明了:這兩局遊戲源自一版 “組合盤”。其實,我是偷了個大懶!一版九方的 “組合盤”,能撰擬出的遊戲 “完整局” 數目,又豈止十個、廿個!你不信,你只要找圖一左、圖二左任何一個,數數剩餘空格,至少還的五十個,不就等如至少可以添加四十九個 “同盤局” 嗎?請記住,只要一格留空就是一局數多酷遊戲吧!因此,數多酷的 “完整局” 數應該遠遠超越 “組合盤” 的總數。 看官,你既有興趣玩數多酷,來之安之,就別走雞下列比賽哦……: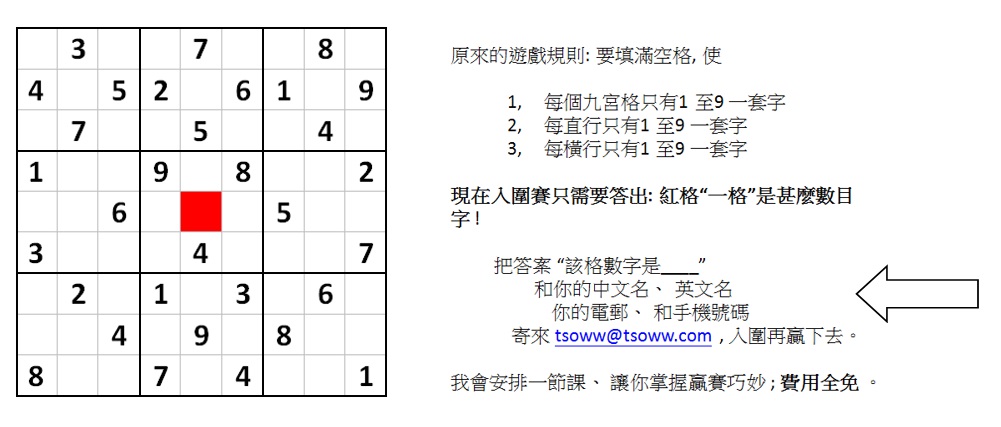
(圖:請註意,只需簽:“該紅格數字為___”)
圖:作者提供 (作者保留版權,引用需得同意;email: [email protected];*本欄不上臉書, 不受點擊統計; 網友查詢需入此頁或電郵) 。 投票已截止,多謝支持